
And like I said, this gives us the conclave up section. We want each double prime to be greater than zero. If we take the first or inventive we have five next to the fourth minus five and the derivative of a constant zero taking the derivative again each double prime iss equal to 20 extra the third and that's it since the derivative vote second term zero.

So for this, we need the second derivative.

Question eight as close to find where the graph each of X is concave up in concrete down. The sandy all the way to 1/2 in conclave, down to the right of one hand. H is Kong cave up to the left of one hand. So if we put that into the second derivative when you get negative six over one, which is is less than C girl. The graph is Conchita and to the right of 1/2. Negative six over negative one, which equals six, which is positive. So we have each double prime of zero is equal to you. You were gonna put that into the second derivative. To left a one, huh? No uneasy one to pick his X equals zero. So first, I'm going to pick a test point. So we want to look both left and right of 1/2 can see what's happening. So that determines how we divide our region. So two X minus one you know can't be zero so x cannot equal 1/2. So this function is undefined where the bottom is equal to zero. So there's no inflection points, but we can find where this function is undefined and use those to determine our intervals. So there's no point where this is equal to zero. So all we have left on the top is a minus six and keep the two x minus one kid. So where's your gun? Um, we have AA minus eight x here, and then we have a minus four times minus two X, which is a positive eight x So those are gone. Um, this top we have on eight X squared and a minus eight x squared. So we're going to go and simplify a little more. And this is all over to X minus one cube.
Calcpad all real numbers plus#
And then we have a or times to X squared nine is two x plus do. So if we foil out his first term, we have I'm eight x squared Greece for X minus another for X must too. So now we can go ahead and keep simplifying. So take one away there, this one goes away and subtract one from the power in the water. I see that every term has a two x minus one so we can go ahead and cancel one. We get to the fourth power and let's go ahead and start simplifying this. Rule tells us to take the derivative of what's inside just just to, and we square what's on the bottom. So it g times f print, which is for X minus two minus f times G prime. So question rule tells us to take being Barton.

The bottom is G and we do the question rule again. So to take the second derivative we need, Teo really believes top Steph. So get to X squared minus two Ex Bastable all over to X minus one squared. And we go ahead and combined terms on the top. Mine is to X minus two ex wired lust, too, and same denominator minus one. So you have two x minus one squared and let's go ahead and simplify this a little bit. So we take G times of Prince minus f times G print, which is just too, and we have GI squared on the bottom.
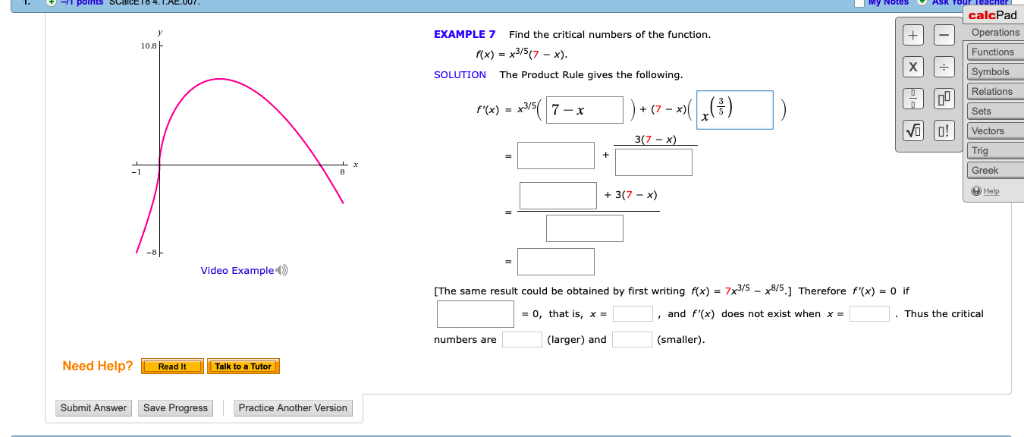
So first, let's find each prime of X, and we need to use quotient rule. So when we're dealing with Khan Cavity, we need to use the second derivative. Push in 14 asked us to find Theo intervals on which the graph is Can't keep up in concrete down.


 0 kommentar(er)
0 kommentar(er)
